OmniSim

Diffraction Grating

Simulation with OmniSim FDTD and FETD software

In this example we use OmniSim's FDTD and FETD Engines to model a diffraction grating with an oblique incidence, and we compare the results with analytical data obtained from the grating equation.

  

Ex component of the nearfield of the a beam of finite width
diffracted from the grating shown live during an FDTD calculation

Different approaches can be used to model such diffraction gratings:

• The FDTD and FETD engines can be used with absorbing boundaries to model the diffraction of a beam of finite width on the grating, which we will study here.

• The FETD and the RCWA engines can be used with Bloch boundaries to model the diffraction of a plane wave on an infinitely periodic grating.

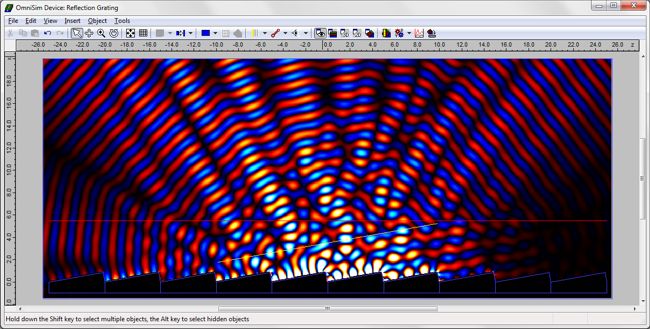
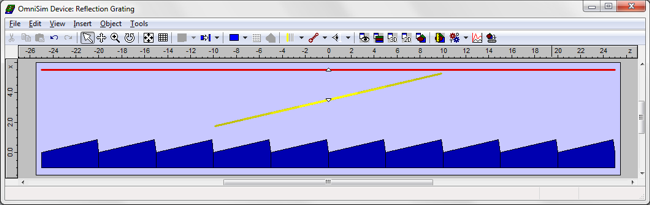
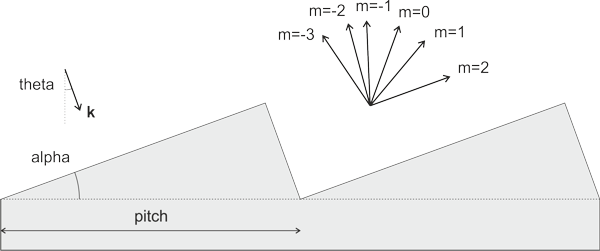
Incident beam of finite width: designing the grating

The design is shown below. The dark blue region corresponds to the silver grating, and the pale blue region to air. We consider ten grating periods, the periodic structure being replicated automatically using OmniSim's sub-device feature. The structure was illuminated with a Gaussian beam (yellow line) and we measured with a sensor (red line) the light radiating from the grating. We used OmniSim's Farfield Calculator to measure the angles at which the radiation was reflected and diffracted.

  

Layout of the diffraction grating designed in OmniSim

The design settings are given in the table below.

  

Schematic view of the grating; k is the wave-vector of the illumination,
the diffraction orders for the reflected beam are shown for theta = 20 degrees

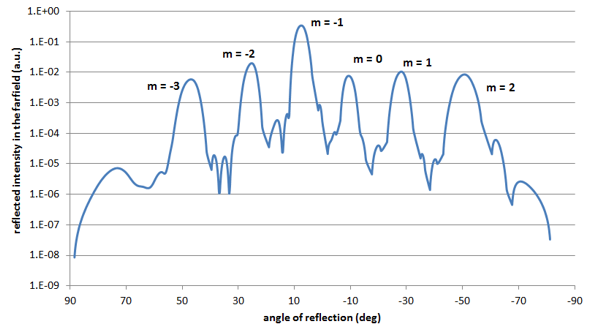
Incident beam of finite width: simulation results with FDTD and FETD

You can see below the farfield plot obtained after the FDTD calculation for light injected normal to the main grating facet, shown in logarithmic scale. The main peak corresponds to the diffraction of order m=-1 at an angle of 7.5 degrees from the normal to the grating, and the other peaks correspond to the different orders of diffraction. Similar results can be obtained from the FETD calculation. The convergence of the results was studied when varying the FDTD grid and the FETD mesh.

  

Farfield of the radiation: intensity plotted versus farfield angle (degrees);
the direct reflection (m = 0) occurs at an angle of -10 degrees

You can see in the table below the theoretical values for the diffraction angles for the different diffraction orders and the calculated values from the FDTD and FETD calculations; all three are in excellent agreement. Note that we use the convention of a positive angle for the direct reflection.

Note that these calculations cannot give you the amount of power coupled to each diffraction order with great precision as we are only considering a finite width of the grating and the peaks are broadened. You would be able to calculate the exact amount of power coupled to each diffraction order with the RCWA engine, which is ideal for such simulations.

The FDTD Engine was able to provide initial results with a very good accuracy in 6 seconds on a computer with a 4-core 7i-2600 CPU; for that simulation we used a grid of 40nm. The FETD Engine was able to provide almost perfectly converged results in 1 minute 40 seconds.

Modelling Echelle gratings and WDM devices

If you are interested in modelling diffraction gratings for use in echelle gratings and WDM Devices, please have a look at Epipprop, our unique echelle grating model.