FIMMPROPA bi-directional optical propagation tool |
   |
Euler Curves and Bent TapersSimulations in fully vectorial 3D with FIMMPROP softwareBasic BendsBasic Bends that have a constant radius of curvature are very simple to model in FIMMPROP. However, despite being very easy to model basic bends of constant curvature have limited use due to their relative efficiency and footprint compared to other types of bend. Variable Curvature BendsFIMMPROP can be used to calculate bends of variable curvature defined either by a mathematical expression or more simply as an Euler Bend. Additionally, FIMMPROP can handle tapers that are bent, allowing transitions for to be minimised in terms of footprint. Previously these features were only possible with a script such as python, but now are easily accessible through the graphical user interface.
Euler BendsEuler bends are often used in photonics to minimises losses whilst also minimising chip footprint. The curvature of the bend varies along its length. In the most basic case the curvature will rise linearly to a maximum and then fall back down linearly to zero as the curve straightens out. A more complex approach is to increase the curvature linearly up to maximum and then continue the bend at this maximum curvature for a given distance before then decreasing the curvature back to zero. The same Euler bend principle is used in civil engineering for bends in highways and on railways. FIMMPROP allows the user to define either a Simple or S-Bend.
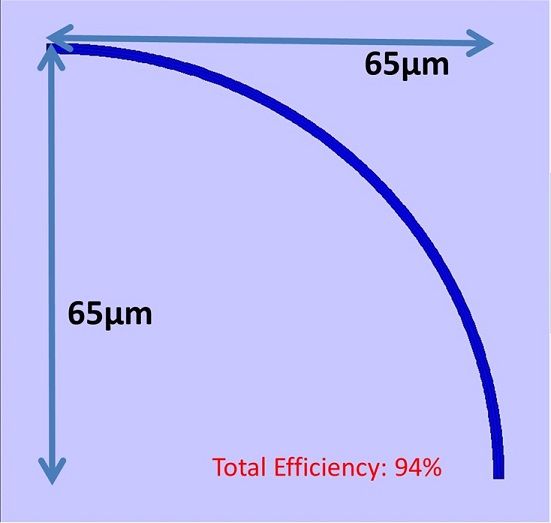
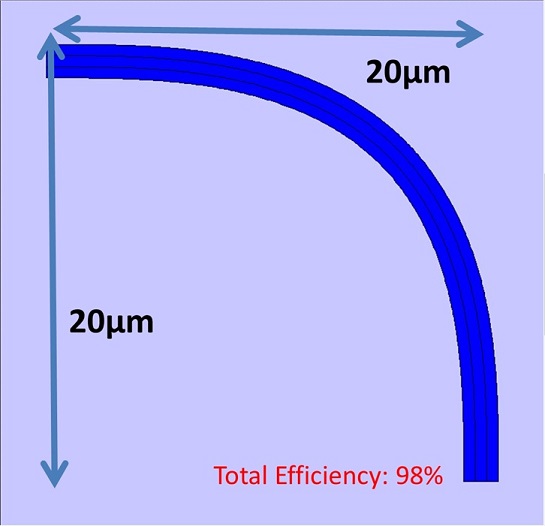
Euler bends typically have a significantly smaller footprint than a basic arc and still achieve the same efficiency. Consider a 90° bend as below in a typical SOI rib waveguide. If this is achieved using an arc then a length and width of 65µm is required to achieve an efficiency of 94%. For the same waveguide a 90° can be made using an Euler curve which has a much smaller footprint of 20x20µm.
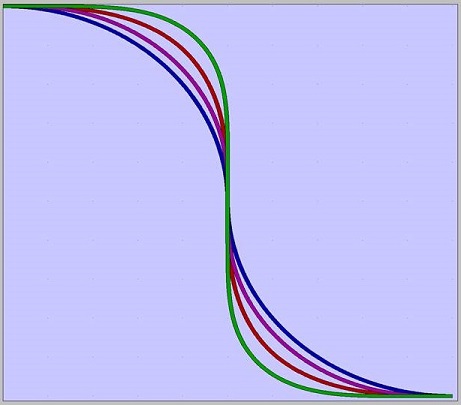
S-BendsFIMMPROP allows the user to compare different bend types. In this brief analysis we shall consider the following types of bends: constant curvature S-bend, Euler S-Bend with 70% constant curvature, Euler S-Bend with 0% constant curvature and an S-Bend with Sin4 curvature. As can be seen in the results table, using a 'partial Euler S-Bend' gives the best transmission efficiency.
Curved Tapers
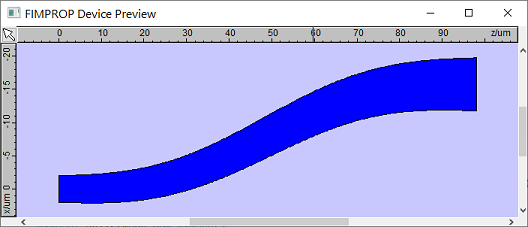
FIMMPROP also allows the user to define a bend which is tapered - the width of the waveguide varies as a function of length. This will allow the design of circuits which have a dramatically reduced footprint.
|