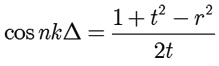OmniSim

Modelling metamaterials using FETD

Simulation of negative index structures with FETD and Bloch boundaries

The FETD engine of OmniSim is well-suited to producing highly accurate results for metamaterial structures involving metallic materials. It has been shown by many authors that suitable subwavelength structures can give rise to emergent negative real parts of the magnetic permeability and even negative real part of the refractive index, the latter giving what is referred to as a negative-index or left-handed material, as originally proposed in [1].

The negative-index property comes from having a negative permeability (via a magnetic resonance) and a negative permittivity (which is naturally the case for many metals). The structures are generically periodic in the transverse direction(s) and thus they were simulated using the Bloch boundary condition of the FETD engine. Only normal-incidence results are shown here, however, oblique incidence can be simulated as easily. 

Note that OmniSim will also allow you to model metamaterials with its 2D/3D RCWA engine.

2D metamaterial structure

A two-dimensional structure, based on [2], was simulated using the 2D FETD engine and the complex coefficients of reflection and transmission (r and t) were measured. From these, the complex effective refractive index of the metamaterial layer was retrieved using the formula 

Two-dimensional metamaterial structure with negative-index property:
(left) the unit cell with silver in red and alumina in blue
(right) z-component (horizontal) of the electric field during the calculation.

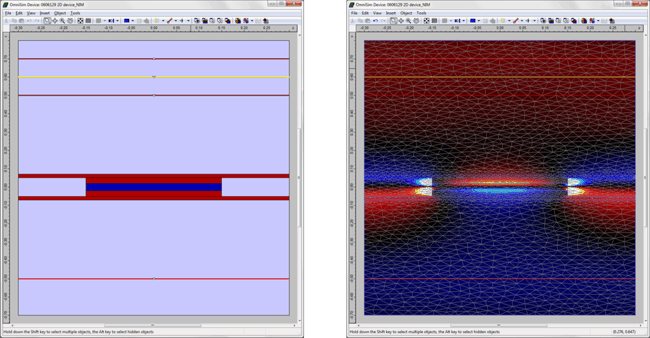
The real part of the refractive index of the metamaterial is shown below; it is negative over the wavelength range 1.4-1.6um (below the dashed red line). Three different element orders were used; the three curves are superimposed, showing that the results are converged to very fine precision.

Real part of the refractive index as a function of wavelength for the above structure.
Negative-index behaviour coincides with a magnetic resonance of the structure.

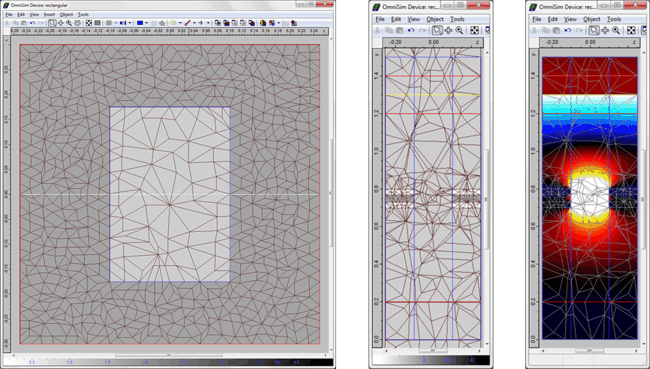
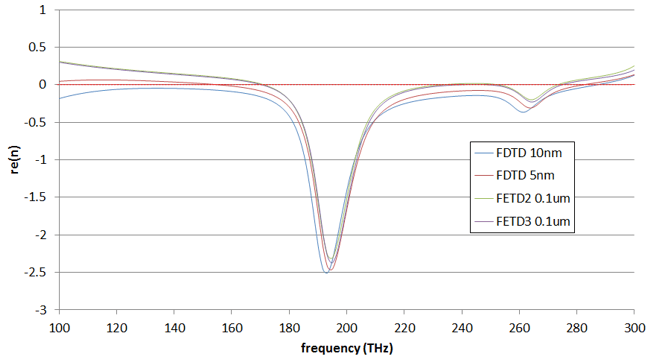
3D metamaterial structure

A three-dimensional "fishnet" structure, based on [3], was simulated. This consisted of a periodic array of rectangular subwavelength holes in a laminate consisting of magnesium oxide sandwiched between two gold layers. The refractive index was retrieved as described above. 

Unit cell of the 3D fishnet structure. In the cross section view (central figure), white regions
are gold and the dark central layer is magnesium oxide. The right hand figure
shows the z-component of the electric field during the calculation.

This structure was simulated using FETD and FDTD; you can see below the real part of the refractive index plotted versus frequency, for two different resolutions of FDTD and FETD. The convergence using FETD was found to be more rapid than for FDTD: the two curves obtained with FETD are superimposed over the quasi-entirety of the spectrum, whilst the FDTD results are changing with resolution and tending towards FETD results.

This demonstrates the effectiveness of FETD for simulations involving metallic structures. Close agreement with results shown in [3] was seen for the wavelength-dependence of the effective refractive index.

Real part of the refractive index as a function of wavelength for the rectangular-
hole fishnet structure, obtained with the FDTD and FETD engines for various resolutions.
The negative-index behaviour (below the dashed red line) can be observed seen in the region of 200THz.

References

[1] "The electrodynamics of substances with simultaneously negative values of ε and μ", Sov. Phys. Usp. 10, 509-514 (1968).

[2] "Negative index metamaterial combining magnetic resonators with metal films", U.K.Chettiar, A.V.Kildishev, T.A.Klar, V.M.Shalaev, (arXiv:physics/0606129).

[3] "What is a good conductor for metamaterials or plasmonics", C.M.Soukoulis, T.Koschny, P.Tassin, N.-H.Shen, B.Dastmalchi, Nanophotonics 2015 4, 69-74.